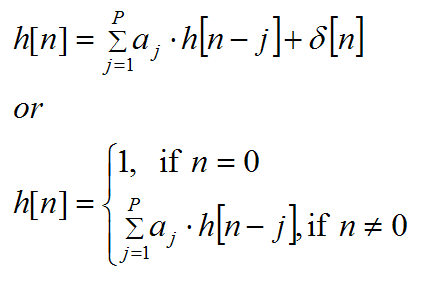
Speech Signal Processing Project-2 Fall 2003
Try to implement the short-term
linear prediction coding (LPC) for speech signals.
You should follow the following instructions:
1. Using the autocorrelation method with
Levinson-Durbin Recursion and Rectangular/Hamming windowing.
2. Analyzing the vowel (or FINAL) portions of
speech signal with different model orders.
(different P, e.g.
P=6,
14, 24 and 128)
3. Plotting the LPC spectra as well as the
original speech spectrum.
4. Using the speech wave file, bk6_1.wav (no header, PCM 16KHz raw data) as the exemplar.
Hints:
1. When the LPC coefficients aj are
derived, you can construct impulse response signal
h[n], 0≤n
≤ N-1 (N:
frame size) by:
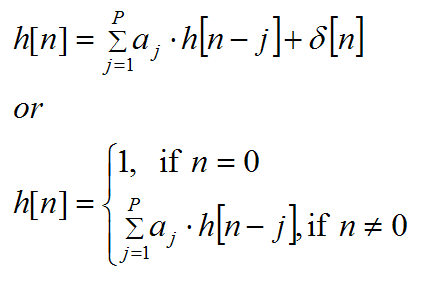
2. The prediction Error E can be expressed by the autocorrelation function:
![]()
3. The MatLab example code:
x=[184.6400 184.1251 . . . . . . . 197.7890 -26.8000 ]; % original signal, dimension: frame size
y=[1.0000 2.0105 . . . . . . . 0.0738 0.0565 ]; % filter's impulse response h[n], dimension: frame size
gain=valG; % valG: the prediction Error E
X=fft(x,512); % fast Fourier Transform, so the frame size < 512
Y=fft(y,512); % fast Fourier Transform
X(1)=[]; % remove the X(1), the DC
Y(1)=[]; % remove the Y(1), the DC
M=512;
powerX=abs(X(1:M/2)).^2; % the power spectrum of X
logPX=10*log(powerX); % the power spectrum of X in dB
powerY=abs(Y(1:M/2)).^2; % the power spectrum of Y
logPY=10*log(powerY)+10*log(gain); %
the power spectrum of Y in dB
% plus gain (Error) in dB
nyquist=8000; % maximal frequency index
freq=(1:M/2)/(M/2)*nyquist; % an array store the frequency indices
figure(1);
plot(freq,logPX,'b',freq,logPY,'r'); % plot the result,
% b: blue line for the power spectrum of the original signal
% r: red line for the power spectrum of the filter
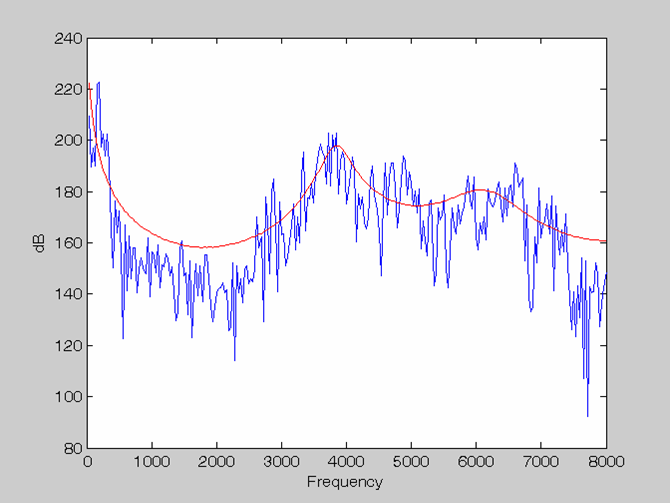
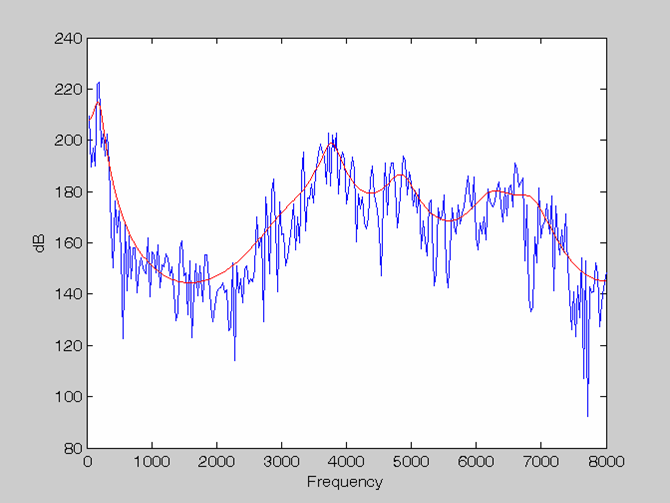
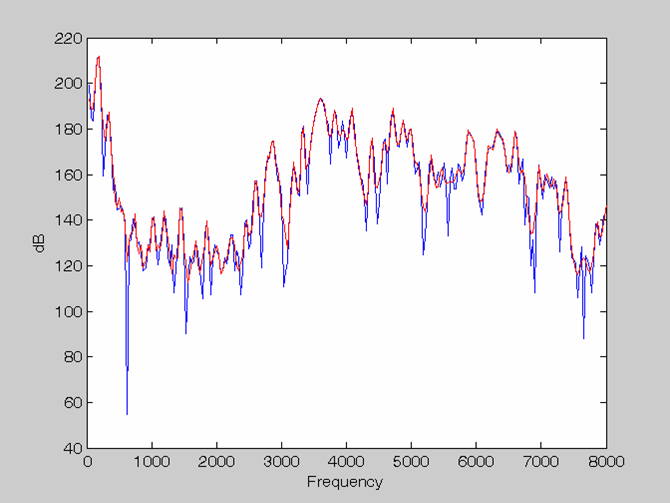
4. Example Figures of LPC Spectra (plotted by Roger Guo, Fall 2002)
|
Order = 6 Rectangle window & no Pre-emphasis |
Order = 14 Rectangle window & no Pre-emphasis |
 |
 |
|
Order = 24 Rectangle window & no Pre-emphasis |
Order = 128 Rectangle window & no Pre-emphasis |
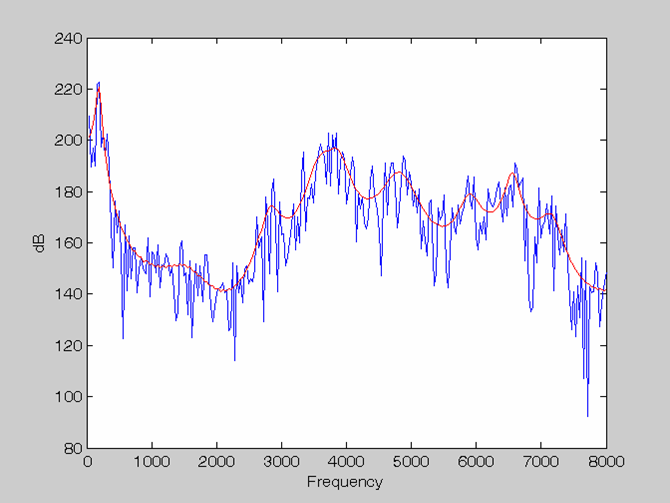 |
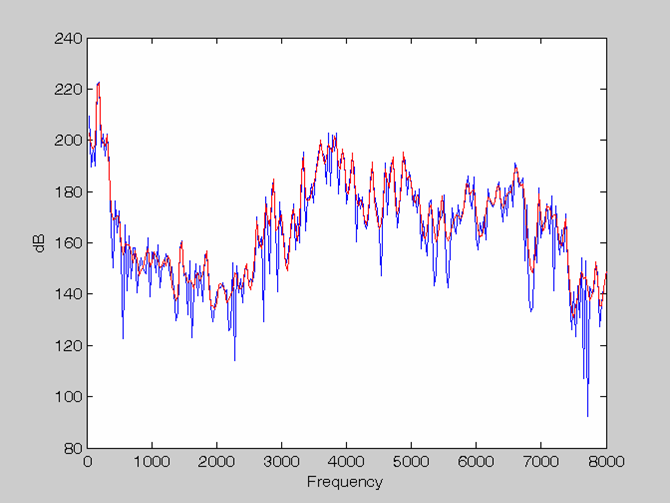 |
|
Order = 128 Rectangle window & Pre-emphasis |
Order = 128 Hamming window & Pre-emphasis |
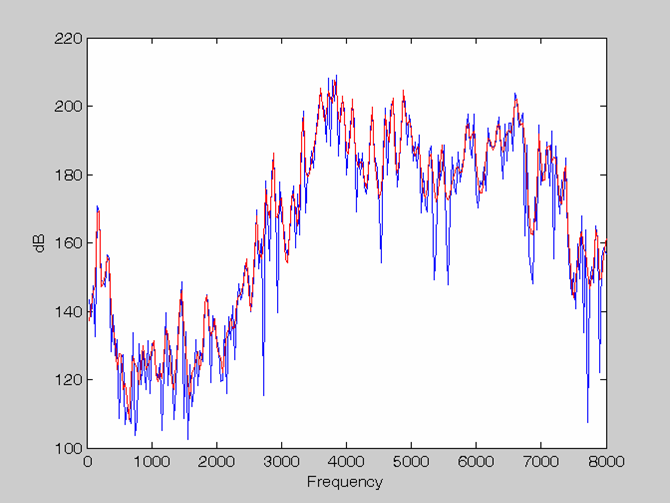 |
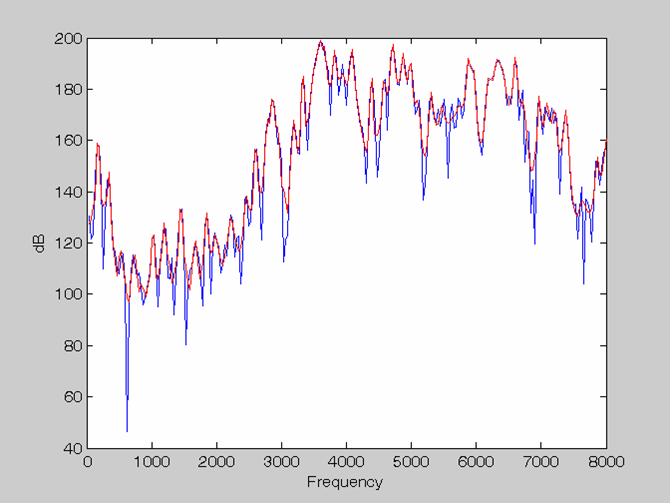 |
|
Order = 128 Hamming window & no PreEmphasis |
|
 |